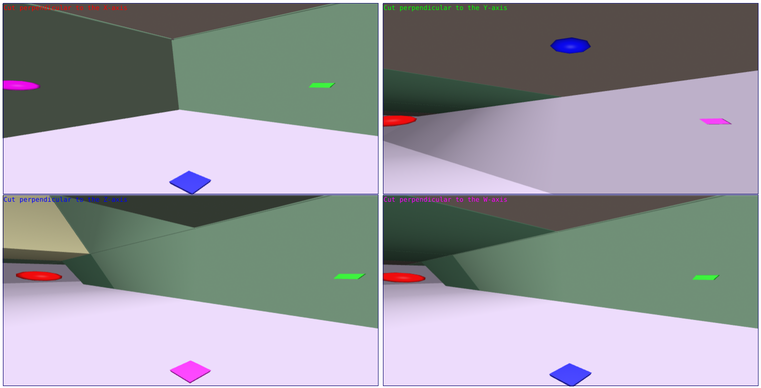
Try to find your way in a 4-dimensional labyrinthe : https://www.raktres.net/tak4d
You are in a 4-dimensional labyrinth,
the objective is to find the yellow hypersphere.

Instructions
You are in a 4-dimensional labyrinth, the goal is to find the yellow hypersphere.
Interface
To understand your environment, you visualize the space through 4 flat cutouts, which are therefore 3-dimensional spaces. These cuts are made perpendicular to the axes of the orthonormal frame O, x, y, z, w and pass through your position.
In the right menu you choose your maze in the top box. Start with the first ones, try random maze when you fell comfortable. The bottom box shows you your position, your last movement as well as the last 20 positions, the most recent first.
In each viewing window, a reticle indicates the axes of the coordinate system along which you can move.
The colors correspond to the axes:
- green – X
- red – Y
- blue – Z
- purple – W
The circle corresponds to the direction of increasing coordinates, the square to the direction of decreasing coordinates.
Moves
You can first look around you. Choose a view, then move the mouse while keeping the left button pressed. As your gaze aims at a point in 4-dimensional space, the 4 views are synchronized to render this movement.
To move around, double-click on the crosshair point indicating the orientation you want to take. You will move forward one square, if the path is free. You cannot exit the gray hypercube, nor go through the walls.
It is also possible to use the buttons in the right panel.
If you prefer the keyboard to move around, the keys are as follows:
- X: up and down arrows
- Y: left and right arrows
- Z: home and end
- W: pageUp and pageDown
Have a nice journey!
Representation of the 4th dimension
If you are a bit lost, here is a quick explanation of the principle used here for visualizing an object in 4 dimensions.
An extension of the principle used in technical drawing
Quick presentation of the technical drawing
To summarize very schematically, the technical drawing allows the representation of an object in 3 dimensions through 3 projections on 3 planes, according to the axes of the orthonormal frame. The projection makes it possible to make volume information disappear, the projection of a volume in 3 dimension is therefore in two dimensions and fits on a sheet. Your shadow on the road is flat.
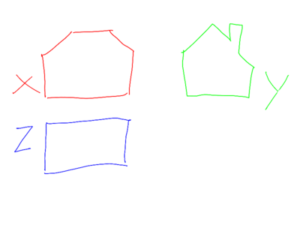
The following animation shows the construction of the representation of a house.

So in the end we have the following representation which makes it possible to reconstruct a mental 3D visualization of the house. These are 3 two-dimensional drawings which schematize the house in 3 dimensions.
This basic principle can be enhanced to show particular details, represent particular shapes. Thus, other projections are possible, particular section planes.
Extension of the principle to the 4th dimension
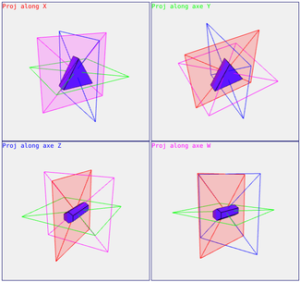
In 4 dimensions, the coordinate system has 4 orientations. To have a complete view it is therefore necessary to make 4 projections, along the 4 axes. And by projecting once we lose one dimension. The result of a projection is therefore an object in 3 dimensions and no longer a plane. It does not fit on a sheet.
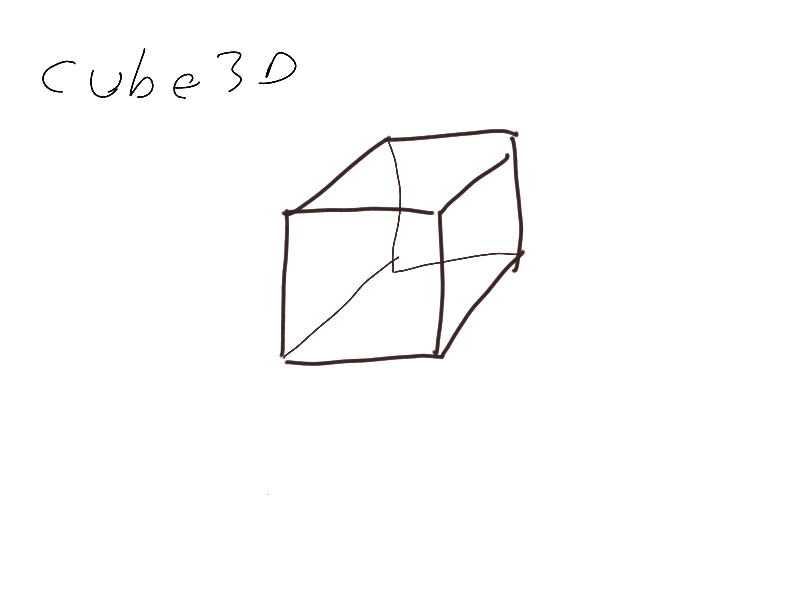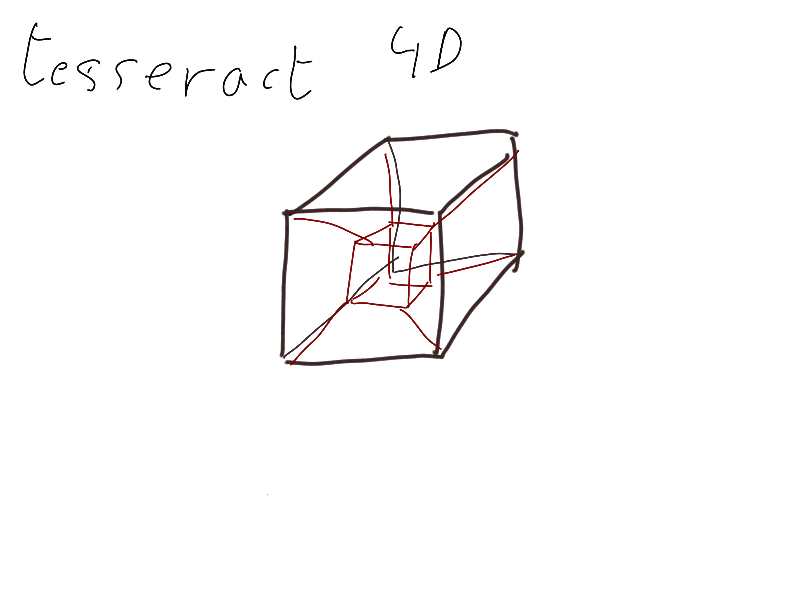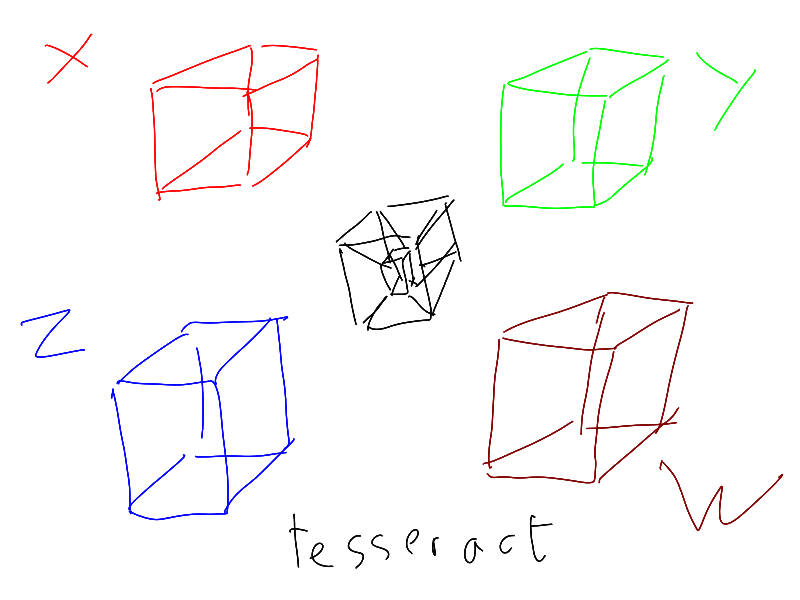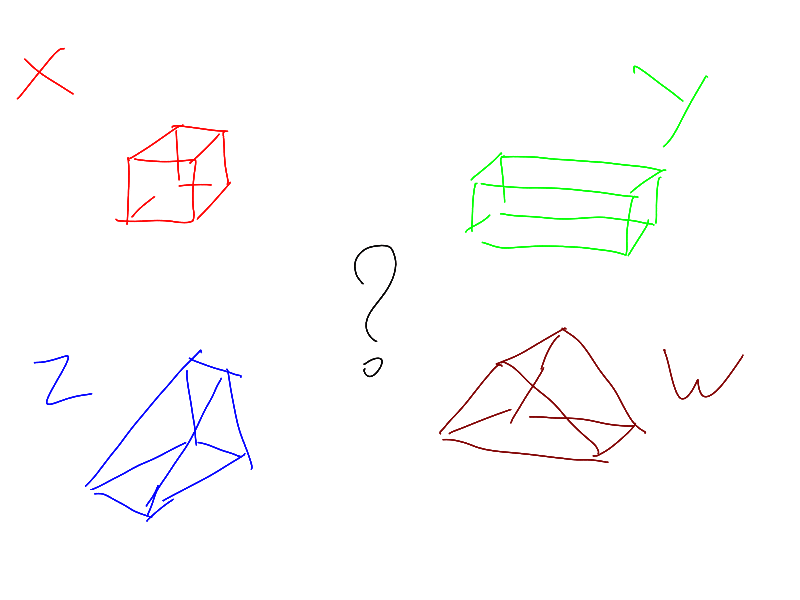
Our 4-dimensional object can be imagined from 4 3-dimensional projections. The blue object is 4-dimensional, and its projections along the 4 axes are represented.
Application for a labyrinth
The limits of the projections
The projections allow you to see the external shapes of objects, but not their interior.
The use of cuts
In order to reveal the interior of an object, we use cuts.
Let’s imagine the following house
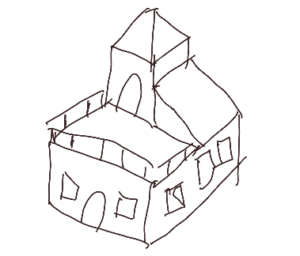
Generally we make plans by floors. The ground floor in figure 1 and the first floor in figure 2.
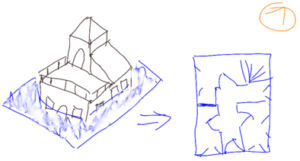
These are horizontal sections which give an idea of the horizontal organization of the house. As the houses are built like stacks of floors, the plans in blue are generally sufficient.
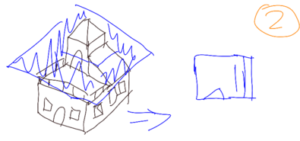
But we could just as easily make vertical sections of the house as in figures 3 and 4.
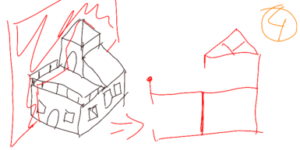
And by making vertical cuts in perpendicular planes we obtain figures 5 and 6.
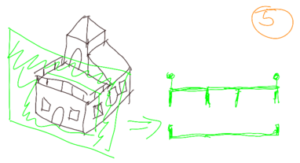
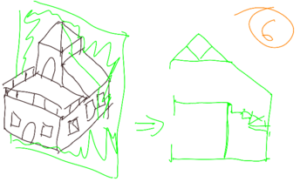
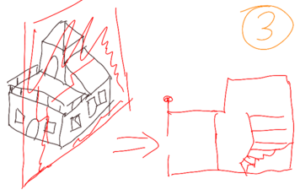
Now that we have the different section views of the house, each room corresponds to a floor plan, and two vertical section views. We can attach these different views to an observer and move it. in the house. Figures 7, 8 and 9 show the association of the plans for 3 rooms.
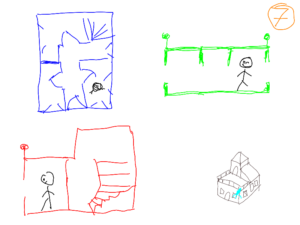
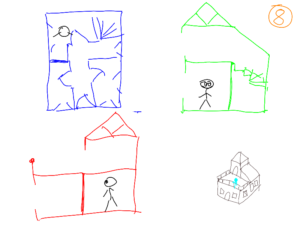
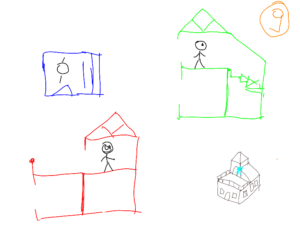
The association of the 3 views during the movement of the man in the different rooms makes it possible to create a 3 dimensional mental image of the house.
The single view by floor is not enough to visualize the small pyramidal roof or the sloping roof.
In picture 8, on the map in red, the man seems locked up. Looking at the green or blue maps allows you to understand that there is a door leading to the corridor.
In figure 7, the steeple is not visible. In fact, no section plane goes through the roof. To see it, you have to change the room.
Extension for a labyrinth in 4D
For a 3D labyrinth, at each position of the observer we can represent 3 sections along the 3 axes. The visualizations are plans in 2 dimensions.
For a 4D labyrinth, at each position of the observer we can therefore represent 4 sections along the 4 axes. The visualizations are 3-dimensional spaces.
- In the section orthogonal to the axis X, we will therefore see the axes Y, Z and W.
- In the section orthogonal to the axis Y, we will therefore see the axes X, Z and W.
- In the section orthogonal to the axis Z, we will therefore see the axes X, Y and W.
- In the section orthogonal to the axis W, we will therefore see the axes X, Y and Z.
As we live in a 3-dimensional space, we cannot see the plane from above in 3D as we did when the projections are in 2 dimensions. We have to immerse ourselves in the plane, we can then turn on itself to look in the different directions. In order to orient oneself, the axes are represented by geometric shapes whose color corresponds to the axis. A sphere corresponds to an orientation with increasing coordinates, a square decreasing coordinates. The red sphere thus represents the direction that it makes increase the coordinates X.